Dr. Peter Niehenke
Stellungnahme zu dem Buch
Die Akte Astrologie von Gunter Sachs
(Goldmann Verlag, München 1997)
Der Anspruch des Buches ist nicht gerade niedrig gesteckt:
- "Die Annahme, daß zwischen Tierkreiszeichen
und menschlichem Verhalten ein Zusammenhang bestehe, war bisher eine
Glaubensfrage. Unvoreingenommen geht Gunter Sachs das Problem nun mit Hilfe
der Statistik an. Und er führt Schritt für Schritt den Beweis:
Astrologie ist kein Mythos. Sie beruht auf meßbaren
Grundlagen." (Klappentext)
Wenn man sich bereits seit langer Zeit mit astrologischer
Forschung beschäftigt, liest man Behauptungen wie diese mit einem
gewissen Erstaunen. Zum einen wird der Eindruck erweckt, dass bisher noch
nie der Versuch gemacht worden sei, mit statistischen Methoden den
Wahrheitsgehalt astrologischer Aussagen zu überprüfen. Zum anderen
wird behauptet, es sei ein "Beweis" geführt worden. Beides ist
aber schlicht falsch.
In den Wissenschaften gilt es nicht ohne Grund als
Selbstverständlichkeit, zu Beginn einer Studie zunächst den
aktuellen Forschungsstand zu recherchieren. Gunter Sachs hat sich anscheinend
mit astrologischer Forschung noch nie beschäftigt ("... aber weder
Cent noch Kopeke wurden meines Wissens je in eine mathematisch-statistisch
fundierte Astrologie-Forschung gesteckt.", (*1), sonst würde er wissen, daß es
Hunderte von statistischen Studien zur Astrologie gibt, die sich
darüberhinaus teilweise, wie bei ihm, auf ein beachtlich umfangreiches
Datenmaterial stützen. Für diejenigen, die sich ein klein wenig
auskennen, mögen das Stichwort "Mars-Effekt" und der Name
Michel Gauquelin als Hinweise genügen. Es hätte seiner Studie
sehr gut getan, wenn er sich mit früheren Versuchen, auf diesem
Wege astrologische Behauptungen zu belegen, ein wenig beschäftigt
hätte. Möglicherweise hätte dies zu mehr Vorsicht, mehr
kritischer Distanz den eigenen Ergebnissen gegenüber geführt, so
daß er der dieser Studie zugrundeliegenden Täuschung weniger leicht
aufgesessen wäre.
Auf der anderen Seite haben in der Wissenschaftsgeschichte
durchaus häufiger sog. "Außenseiter" fundamental neue
Erkenntnisse vorgelegt, die oft genug nur deshalb nicht ernst genommen wurden,
weil es sich eben um "Außenseiter" handelte, die zudem
Erkenntnisse, die zur jeweiligen Zeit vom wissenschaftlichen Establishment
allgemein anerkannt wurden, in Frage stellten. Insofern ist die
fehlende Rezeption bisheriger Ergebnisse astrologischer Forschung durch Gunter
Sachs auch nur von relativer Bedeutung. Die Studie hat es trotz der
beschriebenen Mängel inbezug auf die Wissenschaftlichkeit des
Vorgehens also durchaus verdient, ernsthaft geprüft zu werden.
Dies gilt nicht zuletzt auch deshalb, weil ihr ein für
astrologische Studien sehr ungewöhnliches öffentliches Interesse
zuteil wird. Nicht einmal der renommierte Wissenschaftler Hans-Jürgen
Eysenck erregte in den 70er Jahren dieses Aufsehen, als er eine Studie
vorlegte, die ebenfalls einen Zusammenhang zwischen den Tierkreiszeichen und
menschlichen Eigenschaften nachzuweisen schien. Sachs hat aber wohl mehr Möglichkeiten
publizistischer Art, als es Eysenck hatte (*1). In Sachs' Fall
nehmen sich nun diverse Talk-Shows der Materie an und in Zeitschriften, von
denen man es nicht unbedingt erwarten würde, erscheinen aus Anlaß
dieser Studie ausführliche Interviews mit ihm (*2). Uns Astrologen
könnte eine solche Werbung ja eigentlich nur mehr als willkommen sein,
und so schmerzt es mich ein wenig, daß ausgerechnet ich als Astrologe
gezwungen bin, darauf hinzuweisen, daß die Ergebnisse dieser Studie eine
"Täuschung" sind, die Folge eines Denkfehlers.
Der Fehler ist übrigens recht einfach zu durchschauen:
Nehmen wir an, in einer beliebigen von Gunter Sachs
untersuchten Gruppe (etwa der Selbstmörder) verlaufe die
Geburtenhäufigkeit über ein Jahr hinweg entsprechend der hier
abgebildeten Kurve (die Argumentation ist vom Kurvenverlauf praktisch
unanbhängig und läßt sich auf beinahe jede andere Form des
Verlaufs analog übertragen). (*3)
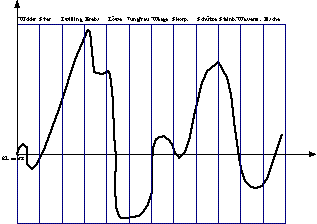 Abbild 1
Die Kurve könnte z. B. so entstanden sein, daß
man für jeden Tag des Jahres die Anzahl der Geburten in der untersuchten
Gruppe in dieses Koordinatensystem einträgt. Die Verbindung dieser 365
Punkte ergäbe dann diese Kurve.
Sachs faßt nun alle Tage, die zu einem bestimmten
Tierkreiszeichen gehören, zusammen, so daß er anstelle der 365
einzelnen Tageswerte jeweils einen Summenwert pro Tierkreiszeichen
erhält. Und anstelle einer Kurve aus 365 Punkten erhält er eine
Kurve aus 12 Punkten, die die Geburtenhäufigkeiten in den 12
Tierkreiszeichen darstellt.
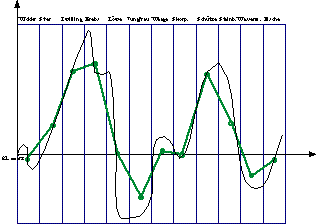 Abbild 2
Wie bei unserer Ausgangskurve (der täglichen
Verteilung der Geburten) auch nicht anders zu erwarten, erhält Sachs nun
natürlich für jedes der 12 Tierkreiszeichen unterschiedliche
Geburtenhäufigkeiten, und die finden wir auch in seinem Buch alle
aufgelistet. Die Unterschiede sind, da die Verteilung in der Tat recht
ungleichmäßig ist, ausgesprochen "signifikant"
(statistisch bedeutsam). (*4)
In der folgenden Abbildung wurde nun anstelle der
Einteilung des Jahreslaufs in 12 Tierkreiszeichen einfach die
Einteilung des Jahres in 12 Monate gewählt. Inbezug auf unsere
Grafik bedeutet das, daß wir unser Raster, das auch in diesem Fall aus
Abschnitten von je 30 Tagen besteht, einfach um einige Tage nach rechts oder
links verschieben (links in der Grafik vom 21. März, dem
Frühlingsbeginn und Beginn des Tierkreises, auf den 1. April). Durch
diese Verschiebung verändern sich natürlich die
Häufigkeiten in jeder dieser 12 Gruppen, d. h. die auf die Monate
bezogenen Häufigkeiten sind selbstverständlich andere als die auf
die Tierkreiszeichen bezogenen Häufigkeiten. Die grüne Linie zeigt
wiederum die neue aus nur noch 12 Punkten bestehende Kurve.
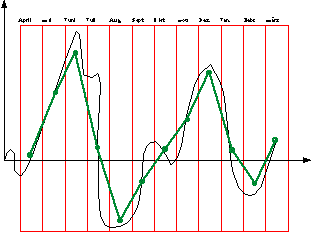 Abbild 3
Auch hier ergeben sich zwischen den 12 Gruppen
hochsignifikante Unterschiede der Häufigkeiten, diesmal beruhend auf den
Monaten anstelle von den Tierkreiszeichen.
Wie man nun leicht sehen kann, würde jede
mögliche Einteilung des Jahreslaufes zu hochsignifikanten
Abweichungen zwischen den einzelnen Gruppen einer solchen Einteilung
führen.
Das ist deshalb so, weil die Verteilung der Geburten über das Jahr eben nicht gleichmäßig ist.
In anderen Worten: Mit der von Sachs gewählten Methode
könnte ich auf der Grundlage des immer gleichen Datensatzes die
Wirksamkeit "völlig gegensätzlicher Einteilungen des
Jahreslaufs beweisen", wenn als Beweis genügen würde, daß
es einfach irgendwelche Abweichungen zwischen den einzelnen Gruppen
gibt. Solche Abweichungen gibt es aber immer, da die Verteilung der
Geburten eben nicht gleichmäßig ist. Man kann also mit dem
vorliegenden Datenmaterial sowohl beweisen, "daß die
Tierkreiszeichen wirken", als auch, "daß die
Monate wirken", als auch, "daß die Stationen des
Indischen Mondkalenders wirken" oder der siderische Tierkreis
anstelle des von Sachs (und den meisten Astrologen) verwendeten
tropischen Tierkreises usw.
Fazit: Gunter Sachs hat durch seine Studie zwar
nachgewiesen, daß die Verteilung der Geburten über das Jahr hinweg
in den von ihm untersuchten Gruppen nicht gleichmäßig ist und von
der statistisch zu erwartenden Verteilung signifikant abweicht. Dies ist
bemerkenswert, nur hat dies (noch) nichts mit den Tierkreiszeichen oder der
Astrologie zu tun! Ob es damit etwas zu tun hat, müßte
gesondert gezeigt werden. So, wie die Ergebnisse von Gunter Sachs jetzt
vorliegen, sind sie zwar statistisch interessant aber
astrologisch irrelevant. Sie sind weit davon entfernt, ein
"Beweis" für die Astrologie zu sein - und ich persönlich
bin auch überzeugt, daß auf der Grundlage dieser Daten nicht die
geringste Chance für einen solchen Beweis besteht.
Meine Überzeugung gründet sich darauf, daß
bei dieser Untersuchung durch die Beschränkung auf das Zeichen der Sonne
(also auf die populäre Tierkreiszeichen-Typologie anhand des
Geburtstags) die biologisch mächtigen jahreszeitlichen Zyklen als
schwer kontrollierbare Stör-Varibalen in die Untersuchung
einfließen. Man kann so die astrologische Typologie von rein
(jahres-)zeitlichen Schwankungen der Geburtenraten nicht trennen. Dies
wäre bei Einbeziehung weiterer astrologischer Faktoren anders, da die
Umlaufrhythmen der Planeten nicht synchron zu diesem, mit dem Lauf der
Sonne zusammenhängenden, besonders mächtigen Rhythmus der
Jahreszeiten laufen.
Wie war dieser Denkfehler möglich?
Gunter Sachs hat sich ja der Mithilfe des Statistischen
Instituts der Universität München versichert. Wie ist es
möglich, daß die Fachleute dort auf meinen hier beschriebenen
Einwand nicht gekommen sind?
Die statistische Auswertung bei dieser Untersuchung ist
sicher fehlerfrei, daran habe ich nicht den geringsten Zweifel. Das Problem,
das ich hier beschrieben habe, ist kein statistisches Problem im
engeren Sinne: Wenn ein Statistiker eine Untersuchung anstellen würde,
wie das Wahlverhalten mit dem Geschlecht zusammenhängt, dann würde
er nie auf die Idee kommen, anhand der Ergebnisse dieser Untersuchung
"beweisen" zu wollen, daß es unterschiedliche Geschlechter
gibt.
Wie hätte man es besser machen können?
Wenn man zeigen würde, daß von allen
möglichen Einteilungen des Jahreslaufes die Einteilung in die
Tierkreiszeichen die signifikantesten Unterschiede bei den
Geburtenhäufigkeiten produzieren, dann wäre dies ein sehr
starkes Argument dafür, daß die beobachtete Ungleichverteilung der
Geburtenhäufigkeiten mit der Tierkreiszeichen-Typologie
zusammenhängen muß. Selbst das wäre ürbrigens, wie jetzt
hoffentlich deutlich geworden ist, noch immer kein "Beweis" - aber
es wäre zumindest ein sehr starkes Argument.
-
Anmerkungen:
-
[*1] "So ganz einfach ist es nicht, hierzulande den
Mitmenschen etwas Lesenswertes zugänglich zu machen - sei es, um sie
aufzuklären, oder nur aus persönlicher Eitelkeit". (Gunter
Sachs in: "Ein Quentchen Wahrheit", DIE ZEIT, Nr. 24, 9. Juni 1995)
-
[*2] "Nach den Sternen greifen", DER SPIEGEL
40/1997, S. 163 ff
-
[*3] Es muß korrekterweise eigentlich heißen:
Die Abweichung von der zu erwartenden Geburtenhäufigkeit",
denn Sachs hat selbstverständlich berücksichtigt, daß die
Geburtenrate in der Gesamtbevölkerung über das Jahr hinweg
auch nicht gleichmäßig verläuft.
-
[*4] Die grün gezeichnete Linie entspricht
übrigens den durchschnittlichen täglichen
Geburtenhäufigkeiten in jeder einzelnen dieser 12 Klassen. Die von Sachs
verwendeten Summen erhält man aus dieser grünen Kurve einfach
dadurch, daß man jeden Wert mit der Anzahl der Tage des entsprechenden
Tierkreiszeichens (also mit etwa 30) multipliziert. Um im Maßstab der
Grafik bleiben zu können, wurde hier der tägliche Mittelwert der
Geburtenhäufigkeit gewählt: Da der Faktor, mit dem man diesen
Mittelwert multiplizieren muß, aber für alle Gruppen in etwa
derselbe ist (immer etwa 30, mal ein Tag mehr, mal ein Tag weniger), bleibt
der Kurvenverlauf dadurch unverändert.
[Siehe auch: ==> "Sachs versus Volkszählung" - Weitere Beispiele zu dieser Stellungnahme]
|













